The Fascinating First-Digit Rule in Data Science
Benford’s Law is an unusual law that exists in the principle in both data science and work in mathematics and forensic accounting. However, it turns out that this mathematical principle predicts pattern of such first digit distribution within many naturally occurring datasets and has turned out to be an extremely effective tool for detecting fraud and data integrity validation and anomaly detection. From tax returns to election results, Benford’s Law is held in use in many areas to detect irregularities in the data pattern. Based on these principles, this mathematical rule is about Benford’s Law that manifests peculiar first digit distribution patterns. The purpose of that essay is to examine several applications of the mathematical trick of the famous Benford’s Law and to show its consequences and limits.
Benford’s Law is a statistical rule that describes how the initial digits actually occur in data collections occurring in real world of data. smaller digits in particular 1 appear much more frequently rather than expected equal appearance patterns, which mean that data follows Benford’s Law. The first digit 1 occurs 30.1 % and the first digit 9 occurs only 4.6 %. Thousands of numerical datasets involving population data as well as river length information, stock figures, and various other scientific constants show a logarithmic first digit frequency pattern.
What makes Benford’s Law so important is that it can be universally applied with little effort. The logarithmical law is a law that applies to data with huge data ranges and is derived from processes of exponential development as well as multiplication. Its application in broad fields in which such patterns are found gives this law broad usefulness; namely in economics as in biology and physics. The analysis tool has the best capability for discovering both the fraudulent activities as well as manipulated data records. When human made numbers are introduced, there are also unanticipated biases that randomize the required Benford statistics.
Despite this, Benford’s Law is a useful tool for many situations and no place for it. There are certain restrictions under which Benford’s Law works perfectly well in use. The regime with which the law optimally functions is one where a dataset extends over many orders of magnitude. Because of this, Benford’s Law does not hold for human heights or shoe sizes, where working with small data sets or data ranges of interest fails. Even if deviations from the expected frequency patterns, by themselves, cannot be proven to be a fraud since they can be due simply to natural dataset uniqueness or external data influences.
Benford’s Law is also one which shares equal importance between human tendencies and mathematical explanations. The mathematical law states that there exists a tendency in nature to keep to the ordered patterns, that despite the fact that humans frequently disturb these patterns. First, Benfords Law generates two essential characteristics that allow for the Benfords Law to be utilized in scientific analysis and investigative auditing as it helps reveal unobservable relationships ofdata. To detect financial crime, to verify authenticity of research and where elections outcomes are in question, Benford’s law provides an advantageous tool for the specialists to use numerical analysis in its unique way, which helps to uncover hidden truths.
The need to discover effective number analysis methods to analyze increasing relevance of big data makes Benford’s Law a very important tool. In this data driven era, we first have fundamental requirement of data accuracy to which is in turn determined the worldwide decision. Benford’s Law, which states that the patterns within seemingly unordered numbers exist, is used to lead the truth seekers to find the real information and expose fraudulent activities in the world. We start our pathway of understanding Benford’s law mathematical structure but seeing its practical use in unveiling concealed information.
What is Benford’s Law?
Benford’s Law, also known as the First-Digit Law, states that in many naturally occurring collections of numbers, the leading digit is more likely to be small. Specifically, the probability that the first digit dd (where dd ranges from 1 to 9) appears as the leading digit is given by:
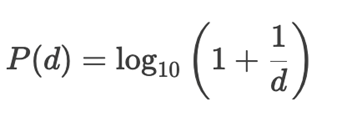
Data shows the appearance rate of 1 at the beginning position exceeds 9 by about 26 times during the set period. The logarithmic distribution pattern appears in datasets covering ranges from one to several orders of magnitude for populations and financial records and river measures. The widespread application of Benford’s Law serves to detect anomalies and uncover fraud and validate data integrity because human-made numbers deviate from its natural distribution format. The analysis tool finds applications in forensic accounting and election analysis because it helps experts find hidden secrets within data collections.
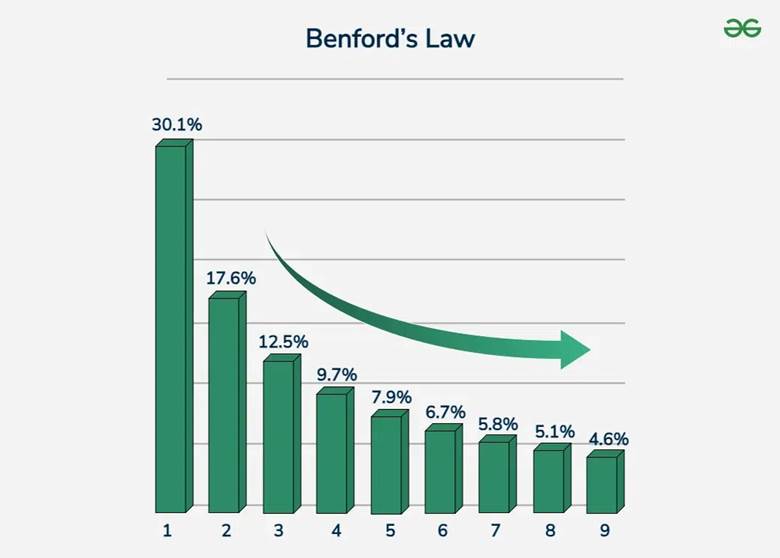
This means that the digit 1 appears as the first digit about 30.1% of the time, while the digit 9 appears as the first digit only about 4.6% of the time. The distribution of first digits according to Benford’s Law is as follows:
| First Digit | Probability |
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
However, first glance at this distribution appears counterintuitive. So that in theory, it should be that each digit from 1 to 9 would have an equal probability to be out first. However, as Benford’s law indicates a natural bias towards smaller digits, and that pattern is found in so many of the real-world datasets, I do not find it appropriate to conclude that something must be going on.
The History of Benford’s Law
Despite being named after physicist Frank Benford, who popularized it in 1938, the phenomenon was first observed by astronomer Simon Newcomb in 1881. At the time that such use was done, logarithm tables were used to make calculations and Newcomb noticed that the pages were more worn for numbers beginning with 1 than for numbers beginning with 9. He stated that there seemed to be more numbers with lower first digits used in calculations.
Newcomb later took this observation further, expanding it on more than 20,000 numbers from many sources including river lengths, population counts, and physical constants. He then found that the first digits of these numbers always followed the distribution of Benford’s Law (logarithmic distribution).
Why Does Benford’s Law Work?
The underlying reason for Benford’s Law lies in the concept of scale invariance and the logarithmic nature of many natural phenomena. Here’s a simplified explanation:
- A dataset containing orders of magnitude is required. For instance, think of the populations of cities to which the numbers of a few thousand to a few million apply. As numbers are spread over such a wide range, it goes without saying that smaller digits will show up more often as leading digits.
- The log nature of Benford’s Law is a consequence of what the numbers grow exponentially. Smaller digits dominate towards the end of the scale in an exponential sequence, while larger digits only become more common the larger the numbers are.
- A lot of natural processes do involve multiplication or percentage growth (e.g. stock prices or bacterial growth). Because these processes tend to follow Benford’s Law by creating a logarithmic distribution of first digits, these processes will tend to produce numbers.
Applications of Benford’s Law
Benford’s Law serves multiple practical applications which extend between financial domains and forensic disciplines. These are the main applications of Benford’s Law:
1. Fraud Detection
Benford’s Law is a foremost method in identifying financial fraud cases. Generally, it is rare for artificial data made out of artificial data made in contravention to natural processes to follow the distribution pattern of first digits because the artificial data was created by means of human intervention in deliberate acts. For example:
Benford’s Law is used to verify the tax declaration by authorities. Auditors compare actual data with the basis because the expected distribution of first digits of reported income or expenses is the basis for the expected distribution of the first digits of manipulations or fraudulent activities.
Accounting fraud examination techniques help financial statement auditors to detect irregularities in a company. Invariably businesses involved in financial data manipulation create figures that are counter to Benford’s Law.
2. Election Forensics
Benford’s Law gives scientists a statistical framework that helps spot voting irregularities in voting tallies. By looking into the vote count in particular regions of the 2009 Iranian presidential election, however, they noticed pronounced deviations from distribution according to Benford’s Law and concluded that voting results had been manipulated.
3. Scientific Data Validation
Benford’s Law allows scientists to have an authentic method to check the accuracy of their research datasets. If a given distribution pattern of data is not matched, there is a failure probably due to problems during data acquisition or processing.
4. Economic and Financial Analysis
Benford’s Law is applied by economists and financial analysts to evaluate macroeconomic statistics such as GDP measurements and stock cost data, and inflation numbers. If the data does not pass exactly by the expected distribution, signals of manipulation, or any potential anomalies, can arise.
5. Forensic Science
Also used by law enforcement agencies to examine a crime report, forensic investigators also use it to interpret bits of DNA and for river length assessment. The law mentions some sequences that are believed to suggest evidence alteration as well as data mistakes.
Limitations of Benford’s Law
Although using Benford’s Law has power, it doesn’t always work in all cases. Benford’s Law is not valid proper for proper application of under some conditions.
- It is said that Benford’s Law applies when the dataset contains multiple orders of magnitude and has full freedom on natural distribution. For data of narrow range like human heights and shoe sizes, the distribution patterns remain consistent, and as per the law, these do not fall under the purview of the law.
- Having substantial datasets is the key to the effectiveness of using Benford’s Law. In random errors within small datasets, which are inherently small, wrong outcomes cannot be expected, giving small datasets poor distribution patterns.
- According to Benford’s Law, the distribution patterns of human numbers which come from human activities should be regular anomalies. Also, rounding techniques are human tendency and the human shows preference for some specific digits.
- Benford’s law deviations certainly do not necessarily indicate fraudulent or erroneous activities. In addition, valid explanations such as original data properties as well as external circumstances may also produce deviations from the data.
How to Apply Benford’s Law
Some steps for proper application of Benford’s Law are:
- Then we use the data collection method to get our analytical dataset. Free spaces should be provided for various orders of magnitude of analyzed data, while being free from artificially restricted ranges.
- We have to apply the initial non zero digit extraction to all the numbers of which we have the dataset.
- Suppose observed frequency count for digits from 1 to 9 when they come out in first positions.
- Run the tests to check if observed first digit frequencies match Benford’s Law predicted values.
- It monitors Measure Deviations to find any large difference between the forecasted statistical pattern and actual data results. As a statistical tool, you should carry out the chi-squared test to find out statistically significant deviations between the actual and predicted data patterns.
- After the discovery of significant deviations, the investigation team should examine irregularities to see what their root causes are. In case significant deviations appear additional analysis through auditing or forensic examination needs to be performed.
Real-World Examples of Benford’s Law in Action
1. Enron Scandal
Benford’s Law was used in the analysis of Enron financial statements during the scandal investigation in order to identify possible fraudulent activities. The fact that financial statements were exhibiting accounting fraud was confirmed by the Benford’s Law deviations in first digit distributions.
2. Greek Economic Crisis
On the other hand, Benford’s Law was applied to investigate Greek macroeconomic data during the Greek economic crisis. They found large deviations from what they expected in the distribution which proved EU deficit targets resulted in data manipulation.
3. COVID-19 Data
Benford’s Law was applied to the reported case numbers from various countries in the COVID-19 pandemic. Some analysts who applied the law data found signs of underreporting or intentional tampering.
Conclusion
Benford’s Law is a mathematical discovery used to make people view surprising structural patterns within naturally developing datasets. The Benford’s Law serves as a very useful forensic tool to discover unsuspected fraudulent activities and to discover irregular data patterns in financial and a medical investigations. When applying Benford’s Law, one needs to exercise caution because Benford’s Law has its limitations with respect to each dataset that is going to be analyzed.
It will ensure the fundamental relevance of Benford’s Law tools to the integrity of data as widespread as possible in the modern life and divination of the underlying numerical realty. This special way of analysis gives the reading to Benford’s Law through which each data scientist, auditor and others will get an insight into numerical stories through the numbers.
References
- Barabesi, L., Cerioli, A., & Perrotta, D. (2021). Forum on Benford’s law and statistical methods for the detection of frauds. Statistical Methods & Applications, 30, 767-778.
- Etim, E. O., Daferighe, E. E., Inyang, A. B., & Ekikor, M. E. (2021). application of benford’s law and the detection of accounting data fraud in nigeria.
- Goodman, W. M. (2023). Applying and Testing Benford’s Law Are Not the Same. Spanish journal of statistics, (5), 43-53.



